Hvordan finne området av en likestillet trekant

Matematikk, og geometri spesielt, ifølgemeningsmålinger av skolebarn, en av de mest utrolige leksjonene, og alt fordi de får deg til å lære et stort antall formler som i 90% av dagens voksne ikke har funnet praktisk anvendelse. Men i et øyeblikk lærer vi formler, løser problemer, gjør likninger ikke for det faktum at de kan være nyttige for oss i livet, men fordi det utvikler tanke og logikk. Selv de gamle greske vismennene sa at det menneskelige intellektet kan måles med kunnskap om matematiske fag. Og siden du bestemte deg for å bli kjent med anvendelsen av formlene for en likemessig trekant - tar vi oss selv i hånd og leser hele artikkelen.
Før du begynner å svare på spørsmålet hvordan du finnerområdet av en ensidig trekant og gå til den praktiske delen av artikkelen, der formler og beregninger er gitt, la oss betegne selve konseptet for oss selv. En likemessig trekant er en trekant hvor to av de tre sidene er like lange som er kalt laterale sider. I tilfelle av en vanlig trekant, hvor alle sider er lik, anses den også som ensidig, men omvendt, når en likestilling trekant anses som riktig - er falsk.
Sidene av trekanten skal utpekes, vi vil gjøre det på denne måten, som vist på bildet nedenfor, hvor: a - sider, b-base og h-høyde.
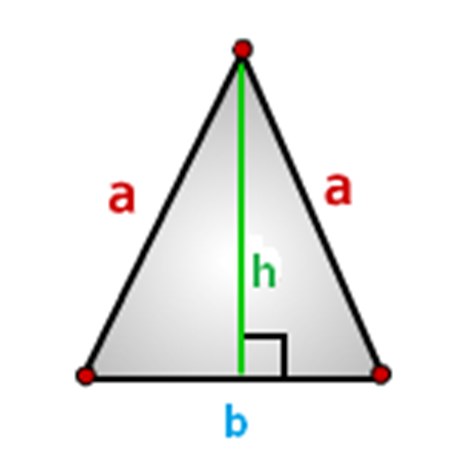
Hvordan beregne området av en likestillet trekant, formler.
Etter at vi har merket høyde, sider og vinkel, kan vi begynne å løse problemet.
Til å begynne med vil vi avgjøre hva vi vet.
Hvis høyden og bunnen - så den klassiske formelen (* - multiplikasjonstegnet):
S = ½ * b * h
La oss erstatte, for eksempel tallene hvor: h = 16, b = 18, vi får følgende:
S = ½ * 18 * 16 = 9 * 16 = 144;
Arealet av en liket trekant er S = 144 cm2
Det finnes andre formler som vil hjelpe ossi hvordan man kjenner området til en likestillet trekant. En slik formel er Herons metode. La oss ikke skrive en kompleks formel, vi tar forkortet en forkortet:
S = ¼ b √4 * a2-b2
Det er klart at b er grunnlaget, og - like sider. Formelen er egnet i tilfelle hvor h-høyden er ukjent.
Ved å erstatte verdiene, la a = 6, b = 3, får vi følgende:
S = ¼ * 3 √4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7
Du kan bruke til å beregne området som er lik sidene av trekanten og vinkelen mellom sidene:
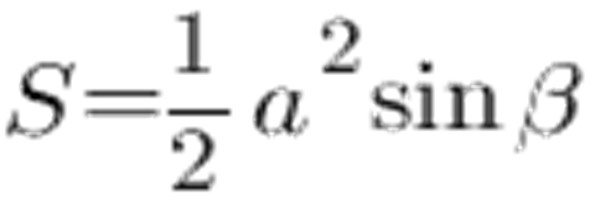
Ifølge sinusbordet er vinkelen ved 45 ° til 0,7071, siden a og la den være 6 cm, får vi følgende:
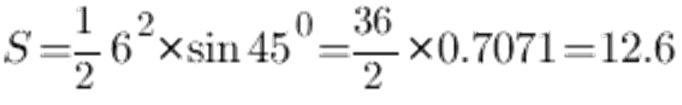
Som et resultat er arealet av en liket trekant 12,6 cm2.
Det finnes også måter å beregne området på, inkludertinkludert i tilfelle av en ensidig trekant, men de er ganske kompliserte og gjelder ikke for "elementære" beregninger, som de som er gitt ovenfor, i begrepet kompleks matematikk. Og det er ikke verdt å snakke om ting som selv lærere med erfaring ikke vil forstå.
Så, du kan puste et sukk av lettelse, på detteet lite kurs av geometri for å finne området av en likemessig trekant vil bli ansett som fullført, og kunnskapen som er oppnådd som følge av å lese artikkelen læres av "fem".














